Programmation fonctionnelle

Le Tictactoe est un jeu très simple, où deux joueurs (X et O) marquent successivement une case dans une grille 3x3. Le gagnant est le premier joueur qui marque trois cases alignées (en ligne, en colonne ou en diagonale). Dans l'illustration ci-dessous, le joueur X a gagné car il a marqué la ligne du milieu.

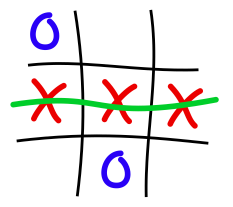
On définit le type Joueur comme un caractère : 'X' pour le joueur X, 'O' pour le joueur O et '.' pour indiquer l'absence de joueur (case libre, pas de vainqueur…).

type Joueur = Char

Ici, on définit le type Joueur comme un synonyme du type Char pour simplifier les affichages mais dans une application réelle, on utiliserait plutôt un type algébrique (mot-clé data).

Un Coup est le numéro (à partir de zéro) de la case choisie dans la grille, en partant du coin haut-gauche et selon le sens de lecture.

type Coup = Int

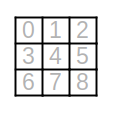
De façon très classique, on stocke la grille dans un tableau 1D, ligne par ligne.

En Haskell, la bibliothèque vector propose une implémentation de tableau 1D efficace. Pour l'importer, on écrit la ligne suivante au début du fichier.

import qualified Data.Vector as V

On peut alors, définir un type de données Tictactoe pour représenter le jeu.

data Tictactoe = Tictactoe
    { grille         :: V.Vector Joueur
    , coupsPossibles :: V.Vector Coup
    , joueurCourant  :: Joueur
    , joueurSuivant  :: Joueur
    } deriving (Show)

Le champ grille contient l'état ('X', 'O' ou '.') des 9 cases de la grille. Le champ coupsPossibles contient les coups restants, c'est-à-dire le numéro des cases à '.' dans la grille. Enfin, les champs joueurCourant et joueurSuivant contiennent les caractères des joueurs courant et suivant.

Initialement, la grille est vide (toutes les cases sont à '.'), tous les coups de 0 à 8 sont possibles, le joueur X commence et le joueur O est le suivant :

jeuInitial :: Tictactoe
jeuInitial = Tictactoe (V.replicate 9 '.') (V.fromList [0..8]) 'X' 'O'

Dans un langage fonctionnel pur comme Haskell, on ne modifie pas une variable mais on en retourne une nouvelle dont le contenu prend en compte la modification voulue. Ainsi pour jouer un coup, on prend un Tictactoe et un Coup, et on retourne le Tictactoe modifié.

jouerCoup :: Tictactoe -> Coup -> Tictactoe
jouerCoup jeu coup =
    if coup `elem` coupsPossibles jeu then jeu' else error "coup invalide"
    where grille' = grille jeu V.// [(coup, joueurCourant jeu)]
          coups' = V.filter (/= coup) (coupsPossibles jeu)
          jeu' = Tictactoe grille' coups' (joueurSuivant jeu) (joueurCourant jeu)

La fonction jouerCoup teste si le coup demandé est possible. Si c'est le cas, on construit et on retourne le jeu modifié, c'est-à-dire avec la case marquée dans la grille, le coup supprimé de la liste des coups possibles et les joueurs courant et suivant échangés. Si le coup n'est pas possible, on considère qu'il s'agit d'une erreur.

Enfin, calculer la fin d'un jeu revient à retourner si le jeu est fini et l'éventuel joueur gagnant, c'est-à-dire un tuple (Bool, Joueur) :

calculerFin :: Tictactoe -> (Bool, Joueur)
calculerFin jeu
    | g!0 /= '.' && g!0 == g!1 && g!1 == g!2 = (True, g!0)  -- ligne 1
    | g!3 /= '.' && g!3 == g!4 && g!4 == g!5 = (True, g!3)  -- ligne 2
    | g!6 /= '.' && g!6 == g!7 && g!7 == g!8 = (True, g!6)  -- ligne 3
    | g!0 /= '.' && g!0 == g!3 && g!3 == g!6 = (True, g!0)  -- col 1
    | g!1 /= '.' && g!1 == g!4 && g!4 == g!7 = (True, g!1)  -- col 2
    | g!2 /= '.' && g!2 == g!5 && g!5 == g!8 = (True, g!2)  -- col 3
    | g!0 /= '.' && g!0 == g!4 && g!4 == g!8 = (True, g!0)  -- diag 1
    | g!2 /= '.' && g!2 == g!4 && g!4 == g!6 = (True, g!2)  -- diag 2
    | null (coupsPossibles jeu) = (True, '.')               -- égalité
    | otherwise = (False, '.')                              -- en cours
    where g = grille jeu
          (!) = (V.!)

Le jeu de Tictactoe étant très simple, on teste ici directement toutes les combinaisons possibles. Pour un jeu plus complexe, on utiliserait évidemment un algorithme plus intelligent.

Le code précédent est suffisant pour dérouler des parties de Tictactoe. Pour cela, on peut lancer l'interpréteur interactif (par exemple, avec l'outil stack), évaluer le jeu initial, jouer un coup…

$ stack repl Tictactoe.hs

*Main> jeuInitial
Tictactoe {grille = ".........", coupsPossibles = [0,1,2,3,4,5,6,7,8], joueurCourant = 'X', joueurSuivant = 'O'}

*Main> jouerCoup jeuInitial 4
Tictactoe {grille = "....X....", coupsPossibles = [0,1,2,3,5,6,7,8], joueurCourant = 'O', joueurSuivant = 'X'}

On peut également profiter du côté haut-niveau du langage. Par exemple, pour calculer le jeu illustré dans la première section, il suffit de calculer la réduction depuis la gauche (foldl) de la liste de coups [4,0,3,7,5] à partir du jeu initial et selon la fonction jouerCoup :

*Main> jeu40375 = foldl jouerCoup jeuInitial [4,0,3,7,5]

*Main> jeu40375
Tictactoe {grille = "O..XXX.O.", coupsPossibles = [1,2,6,8], joueurCourant = 'O', joueurSuivant = 'X'}

Enfin, on peut également tester la fin d'une partie : le jeu initial n'est pas fini, le jeu 4-0-3-7-5 précédent est fini et gagné par le joueur X.

*Main> calculerFin jeuInitial
(False,'.')

*Main> calculerFin jeu40375
(True,'X')

Dans le cas des jeux, une intelligence artificielle (également appelée bot) est simplement une fonction qui prend l'état du jeu courant et retourne un coup à jouer. Cette fonction consiste généralement à regarder les coups possibles, estimer leurs probabilités de donner une victoire et retourner le coup ayant la plus grande probabilité.

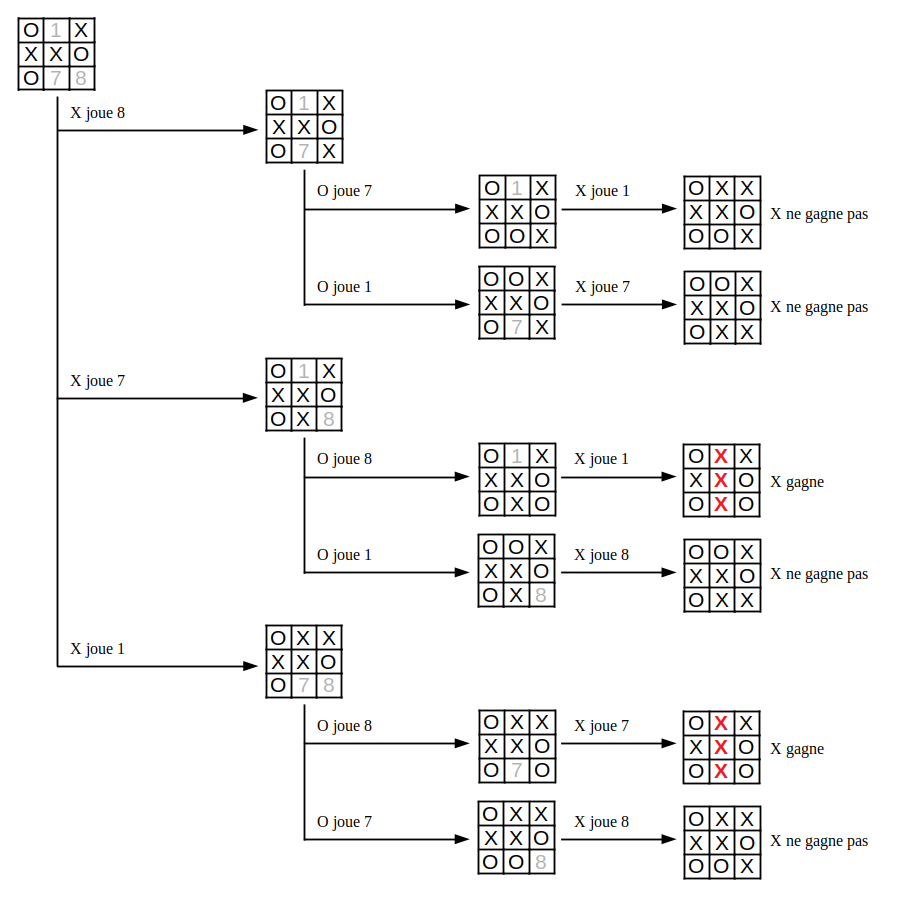
Pour illustrer ça, considérons le jeu 4-0-2-5-3-6 suivant. Ce jeu correspond à la suite de coups [4,0,2,5,3,6] et a comme coups possibles [1,7,8].

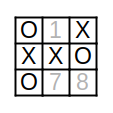
On peut alors détailler toutes les parties possibles à partir de ce jeu. Par exemple, si X joue 7 puis O joue 8 puis X joue 1, alors X gagne avec la colonne du milieu. Par contre, si X joue 7 puis O joue 1 puis X joue 8, alors il y a égalité et X ne gagne pas.

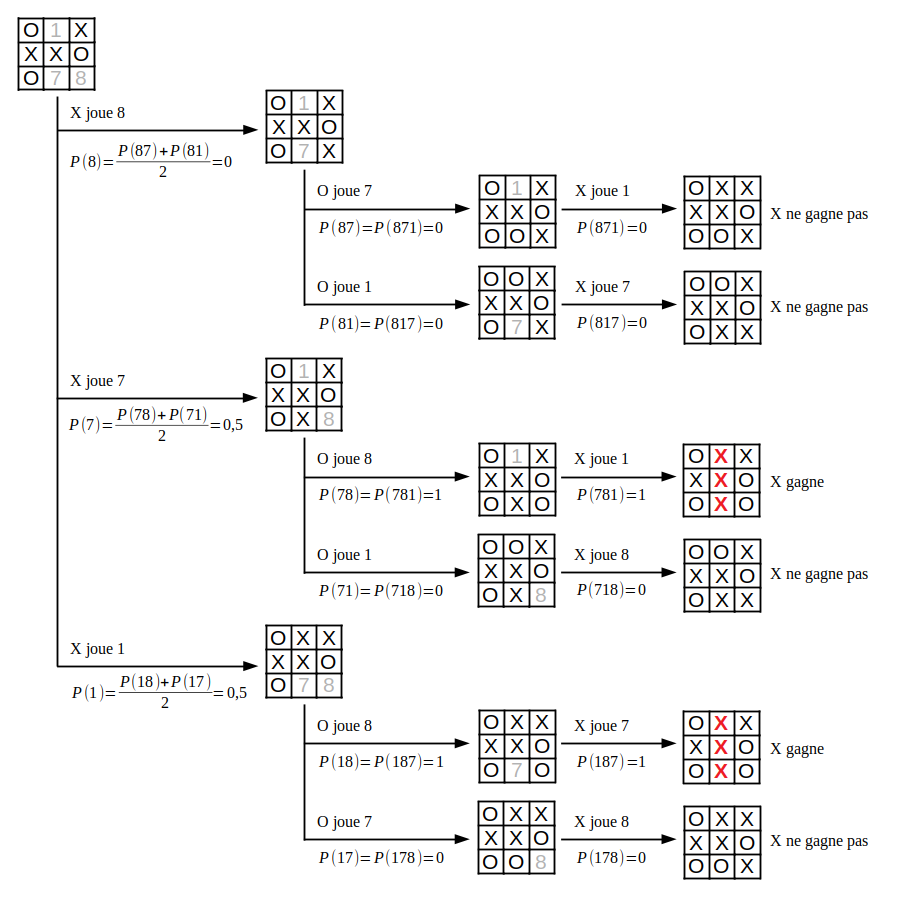
On peut donc calculer les probabilités que le joueur X gagne pour les différentes parties. Par exemple, si X joue 7 puis O joue 8, alors il ne reste qu'un coup possible (X joue 1) et X gagne. On peut donc dire que la probabilité que X gagne après la série de coups 7-8 est P(78) = 1. De même, après la série 7-1, il ne reste que le coup 8 et X ne gagne pas, c'est-à-dire P(71) = 0. En résumé, si on considère que X joue 7 et que O choisit ensuite un de ses deux coups possibles avec la même probabilité, alors la probabilité que X gagne avec le coup 7 est P(7) = 0,5.

Ici, on a développé tout l'arbre de jeu et calculé toutes les probabilités car le nombre de possibilités est faible. Avec des jeux moins triviaux que le Tictactoe, la combinatoire est souvent énorme et il est impossible de calculer exactement les probabilités de victoire. On utilise alors des méthodes approchées, comme Monte-Carlo.

La méthode de Monte-Carlo consiste simplement à estimer la qualité d'un coup en jouant des parties aléatoires à partir de ce coup. La moyenne des parties victorieuses converge vers la probabilité cherchée.

Pour implémenter des IA avec des simulations aléatoires, on a besoin d'un générateur de nombres aléatoires. Haskell propose le type StdGen et la fonction randomR, qui a pour type (en simplifiant) :

randomR :: (Int, Int) -> StdGen -> (Int, StdGen)

La fonction randomR prend un intervalle (Int, Int) et un générateur StdGen, et retourne un nombre choisi aléatoirement dans l'intervalle et le nouveau générateur (Int, StdGen). En effet, comme Haskell est fonctionnel pur, on ne peut pas modifier le générateur pour passer au tirage aléatoire suivant. Pour éviter ce problème, un nouveau générateur est retourné, permettant le tirage suivant.

On peut donc représenter un bot par une fonction qui prend un jeu et un générateur de nombres aléatoires, et retourne un coup à jouer et le nouveau générateur. Pour cela, on définit le type Bot suivant :

type Bot = Tictactoe -> StdGen -> (Coup, StdGen)

On peut alors implémenter un bot qui retourne un coup au hasard parmi les coups possibles.

botRandom :: Bot
botRandom jeu rng = (coup, rng')
    where nbCoups = length $ coupsPossibles jeu
          (iCoup, rng') = randomR (0, nbCoups - 1) rng
          coup = coupsPossibles jeu V.! iCoup

Dans l'interpréteur interactif, on peut tester botRandom sur le jeu 4-0-2-5-3-6 de la section précédente. La fonction getStdGen permet de récupérer le générateur du système. Dans l'exécution ci-dessous, botRandom retourne le coup 8.

*Main> rng0 <- getStdGen

*Main> jeu402536 = foldl jouerCoup jeuInitial [4,0,2,5,3,6]

*Main> botRandom jeu402536 rng0
(8,2084555406 40692)

Pour comparer différentes IA et pour implémenter la méthode de Monte-Carlo, on définit une fonction qui joue un jeu jusqu'à la fin. Cette fonction prend un jeu, deux bots et un générateur de nombres aléatoires, et retourne le joueur gagnant, le jeu final et le nouveau générateur.

jouerJeu :: Tictactoe -> Bot -> Bot -> StdGen -> (Joueur, Tictactoe, StdGen)
jouerJeu jeu botX botO rng =
    if estFini then (vainqueur, jeu', rng') else continue
    where bot = if joueurCourant jeu == 'X' then botX else botO
          (coup, rng') = bot jeu rng
          jeu' = jouerCoup jeu coup
          (estFini, vainqueur) = calculerFin jeu'
          continue = jouerJeu jeu' botX botO rng'

La fonction jouerJeu est récursive : si le jeu est terminé, on retourne les valeurs résultats (vainqueur, jeu', rng'), sinon on retourne l'appel récursif continue. Pour calculer ces valeurs, on demande au bot de choisir un coup, on joue ce coup dans le jeu et on teste si ce nouveau jeu est terminé.

On peut tester cette fonction dans l'interpréteur interactif. Par exemple, l'exécution suivante a fait jouer deux bots aléatoires à partir du jeu 4-0-2-5-3-6 et a donné une égalité :

*Main> jouerJeu jeu402536 botRandom botRandom rng0
('.',
 Tictactoe {grille = "OOXXXOOXX", coupsPossibles = [], joueurCourant = 'O', joueurSuivant = 'X'},
 544765582 2103410263)

Pour évaluer un coup selon la méthode de Monte-Carlo, on définit la fonction evalCoup suivante :

evalCoup :: Coup -> Int -> Tictactoe -> StdGen -> (Int, StdGen) 
evalCoup coup nbSims jeu rng = evalCoupAux 0 nbSims rng
    where joueur = joueurCourant jeu
          jeu1 = jouerCoup jeu coup

          evalCoupAux nbVicts 0 rngAux = (nbVicts, rngAux)
          evalCoupAux nbVicts nbSimsAux rngAux = 
            let (vainq, _, rngAux') = jouerJeu jeu1 botRandom botRandom rngAux
                nbVicts' = if vainq == joueur then nbVicts+1 else nbVicts
            in evalCoupAux nbVicts' (nbSimsAux-1) rngAux'

Comme décrit dans la section précédente, pour évaluer un coup, on commence par jouer le coup dans le jeu initial. À partir de ce nouveau jeu jeu1, on joue ensuite des jeux aléatoires et on calcule le nombre de victoires pour le joueur considéré. Ici, nbSims est le nombre de jeux aléatoires à calculer et evalCoupAux est une fonction locale qui calcule récursivement les jeux aléatoires et le nombre de victoires.

On peut tester cette fonction dans l'interpréteur interactif, par exemple sur le jeu 4-0-2-5-3-6 étudié dans la section précédente.

*Main> evalCoup 8 10000 jeu402536 rng0
(0,826432801 476680813)

*Main> evalCoup 7 10000 jeu402536 rng0
(4965,826432801 476680813)

*Main> evalCoup 1 10000 jeu402536 rng0
(4965,826432801 476680813)

On retrouve bien les probabilités théoriques : P(8) = 0 (0 victoire sur 10k simulations), P(7) ≈ 0,5 (4965 victoires sur 10k simulations) et P(1) ≈ 0,5 (4965 victoires sur 10k simulations).

Enfin, la fonction botMc suivante retourne un bot de type Monte-Carlo dont le budget de simulations aléatoires est donné en paramètres (maxSims).

botMc :: Int -> Bot
botMc maxSims jeu rng = botMcAux (nbCoups-1) 0 0 rng
    where nbCoups = length $ coupsPossibles jeu
          nbSimsParCoup = max 1 $ div maxSims nbCoups

          botMcAux (-1) best _ rngAux = (best, rngAux)
          botMcAux iCoup best vBest rngAux =
            let coup = coupsPossibles jeu V.! iCoup
                (vCoup, rng') = evalCoup coup nbSimsParCoup jeu rngAux
                (vBest', best') = max (vCoup, coup) (vBest, best)
            in botMcAux (iCoup - 1) best' vBest' rng'

Cette fonction répartit le budget de simulations sur les coups possibles (nbSimsParCoup). La fonction récursive locale botMcAux évalue ensuite chaque coup (en utilisant nbSimsParCoup simulations) et retient le coup qui donne le plus de victoires.

Si on teste dans l'interpréteur interactif sur le jeu 4-0-2-5-3-6 avec un budget total de 30k simulations, botMc peut retourner le coup 7 ou le coup 1 (qui ont une probabilité de victoire de 0,5) mais pas le coup 8 (probabilité de 0). Dans l'exécution ci-dessous, on obtient le coup 7.

*Main> botMc 30000 jeu402536 rng0
(7,1356595715 1539624735)

L'implémentation des IA avec des fonctions pures a un inconvénient : il faut transmettre explicitement les générateurs de nombres aléatoires entre les différentes fonctions. En effet, comme les fonctions pures ne peuvent pas faire d'effet de bord, un générateur passé en paramètre ne peut pas être modifié pour avancer dans la suite pseudo-aléatoire. Si un générateur est utilisé plusieurs fois de suite, il générera donc exactement les mêmes nombres.

*Main> botRandom jeu402536 rng0
(7,1297534637 40692)

*Main> botRandom jeu402536 rng0
(7,1297534637 40692)

Dans une application réelle, on « consomme » les nombres aléatoires générés successivement. Ces générations doivent donc être uniques. Avec des fonctions pures, il faut retourner le nouveau générateur obtenu et utiliser ce dernier pour le tirage aléatoire suivant.

*Main> (coup1, rng1) = botRandom jeu402536 rng0
*Main> coup1
7

*Main> (coup2, rng2) = botRandom jeu402536 rng1
*Main> coup2
1

En Haskell, la monade State permet d'implémenter ce genre de comportement de façon assez élégante. C'est ce que décrit la section suivante.

La notion de monade vient de la théorie des catégories et a été popularisée notamment par Haskell. Il s'agit d'une fonctionnalité essentielle du langage, que l'on peut voir comme un patron de conception disposant à la fois d'une justification théorique et d'une implémentation générique.

De façon intuitive, une monade est un contexte de calcul/action, qui permet de définir des calculs/actions successifs se transmettant leur résultat. Par exemple, la monade IO implémente un contexte d'entrées-sorties où les actions successives (entrées ou sorties) peuvent se transmettre des données.

La monade State implémente un contexte d'état qui peut évoluer au cours des actions réalisées. Ceci est particulièrement adapté à notre problème de bots basés sur des simulations aléatoires. En effet, on peut définir un Bot comme une fonction qui prend un jeu de Tictactoe et retourne un coup dans une monade State.

type Bot = Tictactoe -> State StdGen Coup

Ici, le type de retour State StdGen Coup signifie que la fonction retourne une valeur de type Coup dans un contexte State où l'état courant est un StdGen. En d'autres termes, la fonction retourne un coup et a accès au générateur courant, qu'elle peut modifier.

En Haskell, la notation do est un raccourci de syntaxe utilisable sur n'importe quelle monade :

• chaque ligne définit une action successive ;
• l'opérateur <- effectue une action et récupère la valeur produite ;
• inversement, la fonction return crée une action contenant simplement une valeur.

Par exemple, on peut définir le bot aléatoire de la façon suivante :

botRandom :: Bot
botRandom jeu = do
    rng <- get
    let nbCoups = length $ coupsPossibles jeu
        (iCoup, rng') = randomR (0, nbCoups - 1) rng
        coup = coupsPossibles jeu V.! iCoup
    put rng'
    return coup

La monade State définit les fonctions get et put pour récupérer et redéfinir l'état courant. Ici, l'état courant est le générateur de nombres aléatoires courant. On le récupère au début de la fonction avec get, ce qui nous permet de générer un nombre aléatoire, via la fonction randomR. Cette dernière retourne, en plus du nombre aléatoire, le générateur suivant rng'. On redéfinit alors le nouveau générateur courant à rng' avec la fonction put. Ainsi, la fonction botRandom met automatiquement à jour son générateur lorsqu'elle génère un coup à jouer.

La fonction evalState exécute une action de type State à partir d'un état initial et retourne la valeur produite. Par exemple, l'exécution suivante calcule botRandom sur le jeu 4-0-2-5-3-6 à partir du générateur rng0, ce qui donne ici le coup 7.

*Main> evalState (botRandom jeu402536) rng0
7

L'intérêt des monades est qu'on n'introduit pas sauvagement les effets de bord mais qu'on reste dans un cadre contrôlé. Par exemple, si on exécute plusieurs fois botRandom sur rng0, on obtient le même résultat car le générateur courant est modifié à l'intérieur de la monade uniquement.

*Main> evalState (botRandom jeu402536) rng0
7

*Main> evalState (botRandom jeu402536) rng0
7

Le code suivant construit et exécute une action qui appelle deux fois botRandom (avec mise à jour du générateur) et produit une liste contenant les deux nombres aléatoires générés.

*Main> :{
*Main| evalState (do
*Main|     coup1 <- botRandom jeu402536 
*Main|     coup2 <- botRandom jeu402536
*Main|     return [coup1, coup2]
*Main|     ) rng0
*Main| :}
[7,8]

Ici, on a utilisé la notation do pour définir l'action à exécuter mais on peut également utiliser les nombreuses fonctionnalités que Haskell propose pour manipuler les monades. Par exemple, la fonction replicateM exécute plusieurs fois une action et collecte les résultats dans une liste. Ainsi, on peut réécrire l'exemple précédent de la façon suivante :

*Main> evalState (replicateM 2 (botRandom jeu402536)) rng0
[7,8]

La fonction jouerJeu est également plus simple à implémenter en utilisant la monade State. Elle prend désormais un jeu et deux bots et retourne le joueur gagnant et le jeu final, dans une monade State.

jouerJeu :: Tictactoe -> Bot -> Bot -> State StdGen (Joueur, Tictactoe)
jouerJeu jeu botX botO = do
    let bot = if joueurCourant jeu == 'X' then botX else botO
    coup <- bot jeu
    let jeu' = jouerCoup jeu coup
        (estFini, vainqueur) = calculerFin jeu'
    if estFini then return (vainqueur, jeu') else jouerJeu jeu' botX botO

Ici, le générateur de nombres aléatoires est plus simple à gérer : il est pris en compte dans l'état courant (pas de paramètre spécifique à passer) et il est mis à jour automatiquement lorsqu'on demande au bot de générer un coup. Remarque : la syntaxe let à l'intérieur d'un do permet de définir des valeurs pures (sans action).

On peut alors tester jouerJeu dans l'interpréteur interactif. Dans l’exemple suivant, deux bots aléatoires sur le jeu 4-0-2-5-3-6 et à partir de l'état rng0, le joueur X gagne en alignant la colonne du milieu.

*Main> evalState (jouerJeu jeu402536 botRandom botRandom) rng0
('X',Tictactoe {grille = "OXXXXOOXO", coupsPossibles = [], joueurCourant = 'O', joueurSuivant = 'X'})

Pour la fonction evalCoup, avec les fonctions pures, on utilisait une fonction locale récursive qui calculait les simulations successives et transmettait les nombres de victoires et générateurs successifs. La monade State simplifie beaucoup l'implémentation car les générateurs sont gérés automatiquement, et car la fonction replicateM permet d'exécuter directement les actions jouerJeu tout en collectant les résultats dans une liste.

evalCoup :: Int -> Tictactoe -> Coup -> State StdGen (Int, Coup)
evalCoup nbSims jeu coup = do
    let joueur = joueurCourant jeu
        jeu1 = jouerCoup jeu coup
    (, coup) . sum <$> replicateM nbSims (do
                            (vainq, _) <- jouerJeu jeu1 botRandom botRandom
                            return $ if vainq == joueur then 1 else 0)

L'opérateur <$> (également appelé fmap) permet d'exécuter une fonction pure sur le résultat d'une action et de retourner la valeur obtenue dans une autre action. Ici, l'action replicateM retourne une liste de 1 et de 0 qui indique si chaque simulation a donné une victoire ou non. La fonction (, coup) . sum calcule donc le nombre de victoires total puis construit un tuple contenant le nombre de victoires et le coup.

*Main> evalState (evalCoup 10000 jeu402536 1) rng0
(5030,1)

*Main> evalState (mapM (evalCoup 10000 jeu402536) [1,7,8]) rng0
[(5030,1),(4898,7),(0,8)]

La fonction botMc consiste à évaluer tous les coups et à retenir celui qui donne le plus de victoires. Comme les générateurs sont gérés automatiquement, on peut désormais calculer un mapping de evalCoup sur la liste des coups possibles. Cependant, il faut utiliser mapM et non map car evalCoup est une action (dans la monade State) et non une fonction pure.

botMc :: Int -> Bot
botMc maxSims jeu = do
    let coups = coupsPossibles jeu
        nbCoups = length coups
        nbSimsParCoup = max 1 $ div maxSims nbCoups
    snd . maximum <$> mapM (evalCoup nbSimsParCoup jeu) coups

Comme pour evalCoup, on utilise l'opérateur <$> pour appliquer une fonction sur la liste des résultats : récupérer le tuple (nombre de victoires, coup) qui a le plus grand nombre de victoires puis retourner son second élément, c'est-à-dire le coup.

*Main> evalState (botMc 10000 jeu402536) rng0
7

Pour plus d'information sur la monade State, voir le wikibook Haskell ou la documentation du module Control.Monad.State.Lazy.

Dans cet article, nous avons vu le principe de l'IA Monte-Carlo et comment l'implémenter avec le langage Haskell, pour le jeu de Tictactoe.

La méthode de Monte-Carlo consiste à calculer des simulations aléatoires pour estimer la valeur des coups possibles, sans avoir à développer et à analyser tout l'arbre de jeu. C'est une méthode simple mais qui est à la base de méthodes modernes performantes. Par exemple, la méthode de Monte-Carlo Tree Search calcule les parties intéressantes de l'arbre de jeu grâce à des simulations aléatoires. Couplée à des réseaux de neurones profonds, cette méthode est à la base de l'algorithme d'AlphaGo.

La méthode de Monte-Carlo s'implémente facilement en Haskell mais la gestion des nombres aléatoires est un peu fastidieuse. En effet, lorsqu'on tire un nombre aléatoire à partir d'un générateur, on récupère également un nouveau générateur, pour les tirages suivants. Ainsi, chaque fonction qui, directement ou indirectement, effectue des tirages aléatoires doit prendre un générateur en paramètre et retourner le générateur suivant.

Pour éviter d'avoir à transmettre, entre les différentes fonctions, les générateurs successifs, on peut utiliser la monade State et définir un état courant, ici le générateur courant. Il suffit alors d'implémenter les fonctions dans la monade State pour avoir un générateur courant qui se transmet automatiquement entre les différentes fonctions. L'implémentation obtenue est plus élégante et plus concise (environ 70 lignes de code, jeu + IA).

Pour terminer, on notera que la notion de monade permet, de façon plus générale, de définir un contexte d'actions successives pouvant produire des valeurs. Par exemple, la monade State définit un contexte d'état courant et la monade IO un contexte d'entrées-sorties. Il est également possible de définir de nouvelles monades. Enfin, Haskell propose des fonctionnalités générales pour manipuler les monades (notation do, fonctions replicateM et mapM…). Tout ceci s'intègre dans le système de types et profite donc des vérifications du compilateur.